Область интегрирования образована цилиндрической поверхностью.
В сферической системе координат положение точки Р (x, y, z) в пространстве определяется
тремя числами r, j, q, где r – расстояние от начала координат до точки Р, j - угол между
осью Оx и проекцией радиуса-вектора ОР точки Р на плоскость Оху, а q - угол между осью Oz
и радиусом-вектором ОР точки Р, отсчитываемый от оси Oz (рис.6). Тройка чисел r, j, q





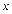
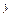
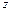
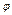
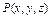
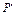

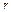



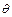 называется сферическими координатами точки Р.
называется сферическими координатами точки Р.
Ясно, что 0 £ r < +¥, 0 £ j < 2 p, 0 £ q £ p.
Координатные поверхности в этой системе координат:
r = const – сферы с центром в начале координат;
j = const – полуплоскости, исходящие из оси Oz;
q = const – круговые конусы с осью Oz.
Рис. 6.
Из рисунка видно, что сферические и декартовы координаты связаны
следующими соотношениями:
| x = r sin q cos j, y = r sin q sin j, z = r cos q. |
Якобиан данной системы функций
J = 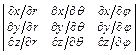 =
= 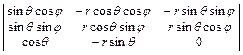 = r 2 sin θ.
= r 2 sin θ.
Следовательно, | J | = r 2 sin θ и формула (2) в данном случае принимает вид
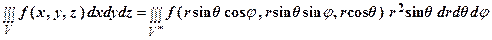 , (4)
, (4)
Выражение dv = r 2sin θ dr dθ dφ называется элементом объема в сферических координатах.
|
|
|
Замечание. Переходить к сферическим координатам удобно, когда область интегрирования
есть шар (уравнение его границы х 2 + у 2 + z 2 = R 2 в сферических координатах
имеет вид r = R) или его часть, а также если подынтегральная функция имеет
вид f (х 2 + у 2 + z 2).
Пример 4. V – область в пространстве, ограниченная сферой x 2 + y 2 + z 2 = 2 az и двумя коническими
поверхностями x 2 + y 2 = z 2 tg2 α, x 2 + y 2 = z 2 tg2 β (0 < α < β < π /2).
В сферических координатах r, φ, θ область V имеет вид V = {0 ≤ r ≤ 2 a cos θ, 0 ≤ φ ≤ 2 π, α ≤ θ ≤ β }.
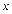
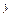
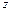
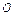

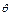









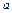
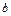 Следовательно,
Следовательно, 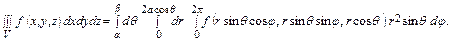
Пример 5. Найти объем выпуклого тела Ω, вырезанного из конуса x 2 + y 2 = z 2
концентрическими сферами x 2 + y 2 + z 2 = а 2 и x 2 + y 2 + z 2 = b 2(a < b).
Переходим к сферическим координатам: x = r sin q cos j, y = r sin q sin j,
z = r cos q. Из первых двух уравнений видно, что a ≤ r ≤ b. Из третьего находим
пределы изменения угла θ: r 2sin2 q = r 2cos2 q => tg q =1, q = π /4, т.е.
0 ≤ θ ≤ π /4 => V = || f (x, y, z) = 1 || = 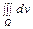 = || J = r 2 sin q || =
= || J = r 2 sin q || =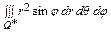 =
=
=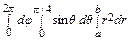 = 2 π ·
= 2 π · 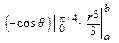 = 2 π
= 2 π 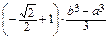 =
= 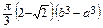 .
.
 2014-02-12
2014-02-12 2958
2958








