В неразветвленных цепях второго порядка

Переходные процессы в цепях второго порядка описываются линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами, имеющим в общем случае вид

Принужденную составляющую решения этого уравнения ищут в виде, подобном его правой части, а свободную составляющую в виде

где pi и рч — корни характеристического уравнения цепи a ₂p²+ a ₁p+ a ₀=0;

A ₁и A ₂ — постоянные интегрирования, определяемые начальными условиями в цепи.

Методику анализа переходных процессов в неразветвленных цепях второго порядка рассмотрим на примере цепи, состоящей из последовательно включенных элементов r, L и С,

13.4.1. Свободные напряжения и токи в цепи rLC

Свободные напряжения и токи в цепи, состоящей из последовательно включенных элементов r, L и С, могут возникнуть, например, при подключении конденсатора С, предварительно заряженного до величины источника э. д. с. E, к цепи с последовательным соединением элементов r и L (рис. 13.15). В соответствии со вторым законом Кирхгофа для получившейся при этом цепи можно записать

Учитывая, что , и , получим

Разделив это уравнение на LC, будем иметь

Обычно вводят обозначения:

При этом уравнение (13.40) будет иметь вид

Характеристическое уравнение, соответствующее выражению (13.41),

имеет корни

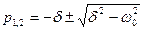, (13.42)

а решение уравнения (13.41) имеет вид

(13.43)

Для определения постоянных интегрирования воспользуемся начальными условиями: u _с(0)=Е и i (0)=0.

Подставив первое начальное условие u_c(0)=E в выражение (13.43), при i =0 получим

. (13.44)

Для того чтобы использовать второе начальное условие, запишем выражение для тока в цепи с учетом формулы (13.43):

Подставив сюда i (0) =0, при t =0 получим

. (13.45)

Решив систему уравнений, состоящую из выражений (13.44) и(13,45), будем иметь;-

Подставив это вформулу (13.43), получим

Ток в цепи

Так как произведение корней р ₁и р ₂характеристического уравнения равно его свободному члену, т. е. р ₁ р₂= 1/ LC, то

При этом напряжение на индуктивности

Характер изменения свободного тока г, напряжений на емкости и_с и на индуктивности u_l зависит от вида корней р ₁и р₂, которые определяются параметрами цепи и ногут быть:

1) вещественными и разными, если δ>ω₀ или r/2L> , откуда r >2ρ, где ;

2) комплексно-сопряженными, если δ<ω₀ или r <2ρ;

3) вещественными и равными, если δ= ω₀ или r =2ρ.

Рассмотрим эти возможные три случая.

1. r >2ρ. В этом случае, как видно из выражений (13.46) — (13.48), свободные напряжения и ток являются суммами двух экспонент (рис. 13.16). Ток не меняет знака, т.е. является апериодическим. Поэтому и рассматриваемую цепь в этом случае называют апериодической.

2. r <2ρ. Для получения закона изменения тока в этом случае в выражении для корней характеристического уравнения (13.42) введем обозначение .

При этом получим

. (13.49)

Подставив это в формулу (13.47), будем иметь

Обозначив , получим

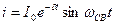. (13.51)

Из полученного выражения, а также из графика, приведенного на рис. 13.17, видно, что свободный ток в цепи в рассматриваемом случае изменяется по закону.затухающих.колебаний. Поэтому и контур rLC в рассматриваемом случае называют колебательным контуром. Скорость затухания колебаний определяется экспоненциальным множителем ,где коэффициент является коэффициентом затухания.

Частота колебаний свободного тока в контуре сосв, называемая также собственной частотой контура, зависит от параметров контура:

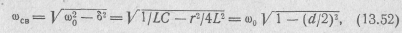
где -резонансная частота;

— затухание.

Затухание d контуров, применяемых на практике, обычно мало. Поэтому в большинстве случаев можно считать, что , т. е. частота свободных колебаний контура равна его резонансной частоте.

Отношение двух следующих друг за другом максимальных значений тока одного знака (см. рис. 13.17) называют декрементом колебания:

где —период свободных колебаний..

Величину, равную натуральному логарифму от декремента колебания, называют логарифмическим декрементом колебания:

. (13.54)

Для получения закона изменения и_с в рассматриваемом случае подставим формулу (13.49) в выражение (13.46). При этом: получим

Представив в виде

Аналогичным образом, воспользовавшись формулой (13.48), можно получить выражение закона изменения напряжения на индуктивности

З. r =2ρ. Законы изменения свободных напряжений и тока в рассматриваемом случае можно найти, перейдя к пределу колебательного разряда емкости, когда . Воспользовавшись выражением для тока (13.51) и учтя, что при , получим

Напряжение на индуктивности

Напряжение на емкости можно найти из основного уравнения цепи :

Подставив сюда выражения (13.57) и (13.58) и учтя, что , получим

. (13.59)

График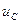и , i и , в рассматриваемом случае будут иметь такой же вид, как и в первом случае (см. рис. 13.16). Ток не меняет знака, поэтому процесс в цепи является апериодическим. Рассматриваемый процесс в цепи называют критическим, так как он является граничным между апериодическим и колебательным процессами. Длительность переходных процессов в этом режиме будет наименьшей. Сопротивление r =2ρ называют критическим сопротивлением.